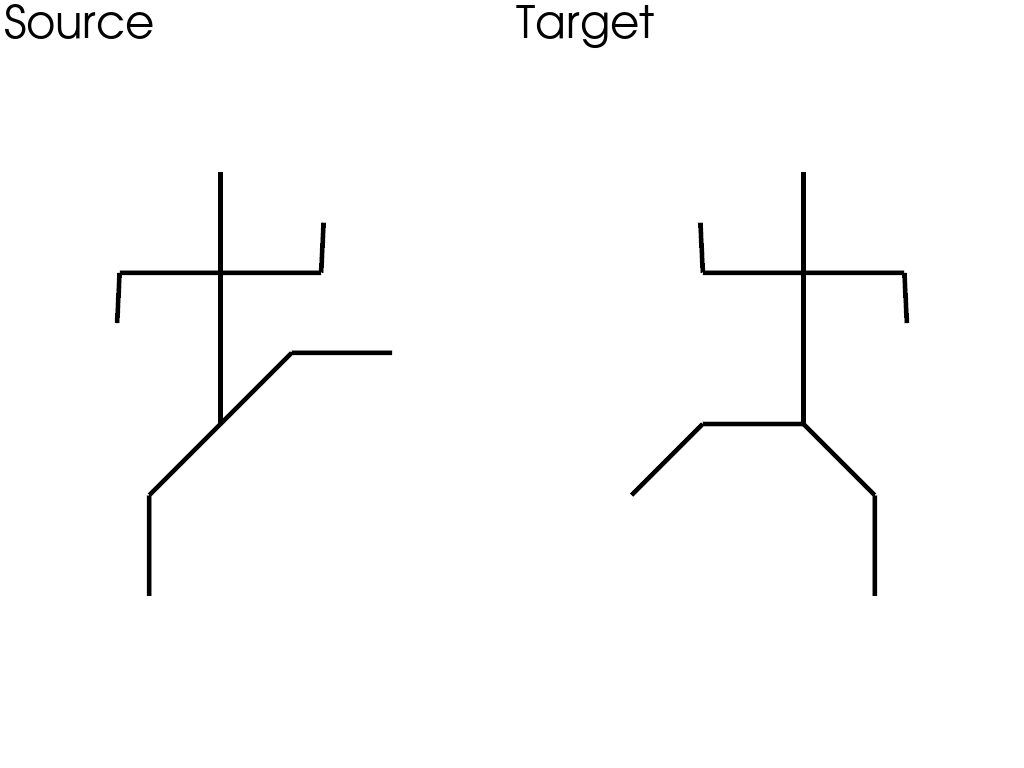
Intrinsic vs Extrinsic deformation

Intrinsic and extrinsic deformations are two different approaches to non-rigid deformation.

This example shows how both approaches differ on a simple 2D example.

import sys

import pykeops
from utils_karateka import (
    load_data,
    plot_extrinsic_deformation,
    plot_intrinsic_deformation,
    plot_karatekas,
)

import skshapes as sks

sys.path.append(pykeops.get_build_folder())

kwargs = {
    "loss": sks.L2Loss(),
    "optimizer": sks.LBFGS(),
    "n_iter": 5,
    "gpu": False,
    "verbose": True,
}

Load the data

source, target = load_data()
plot_karatekas()

Static Scene

Interactive Scene

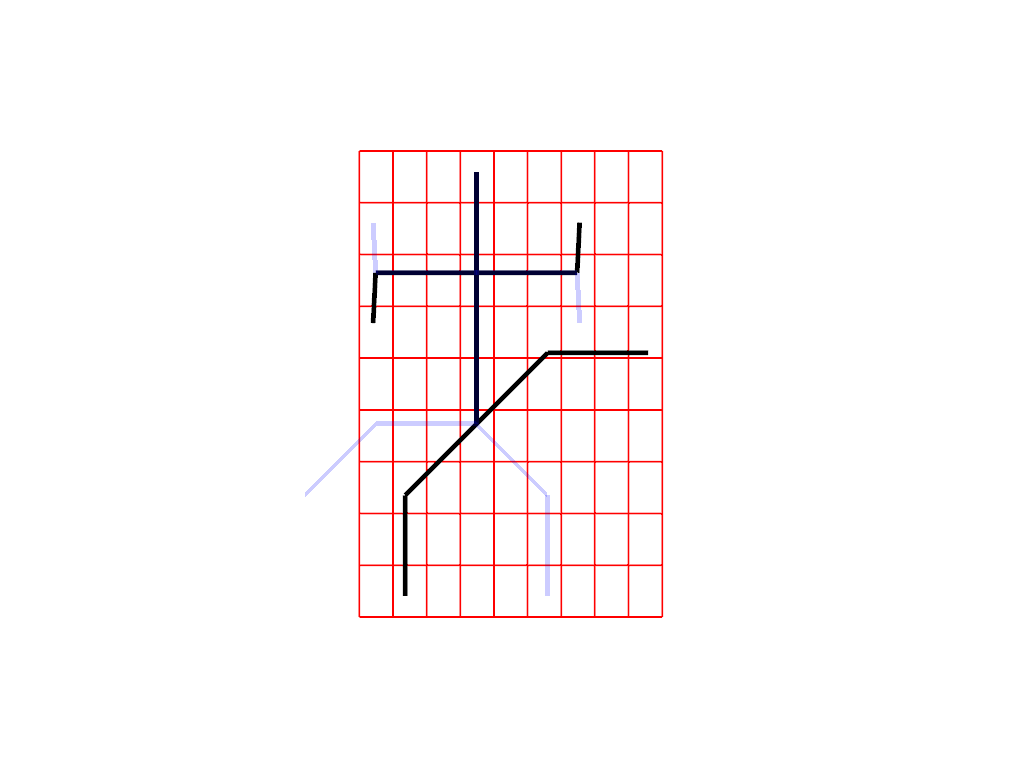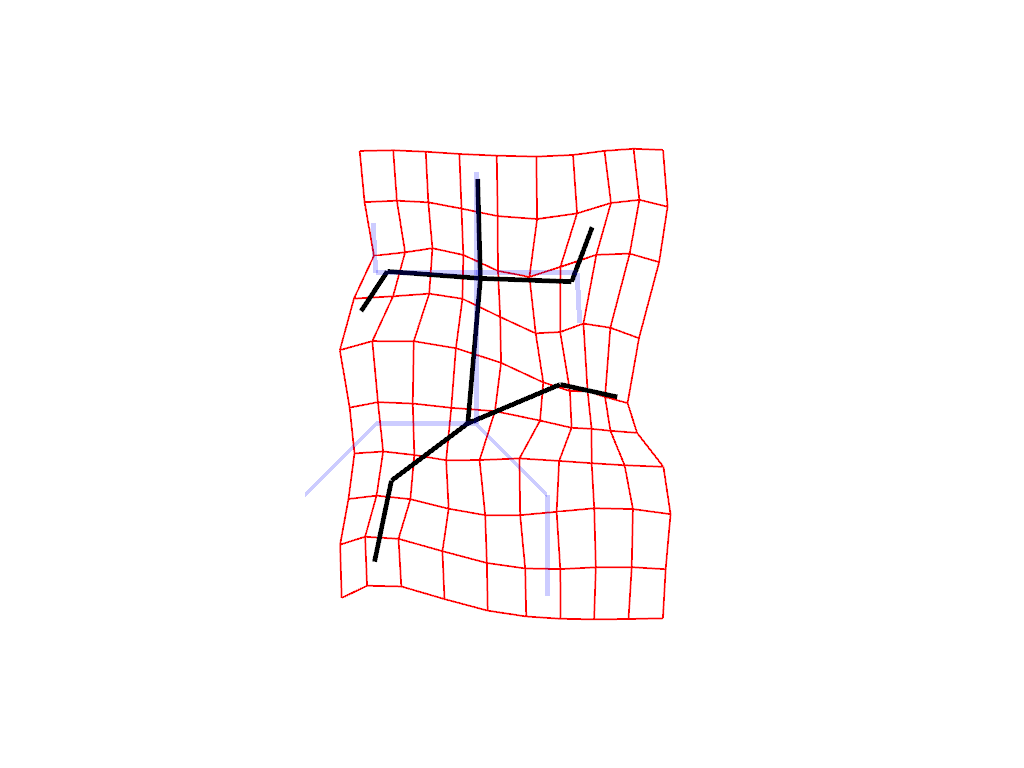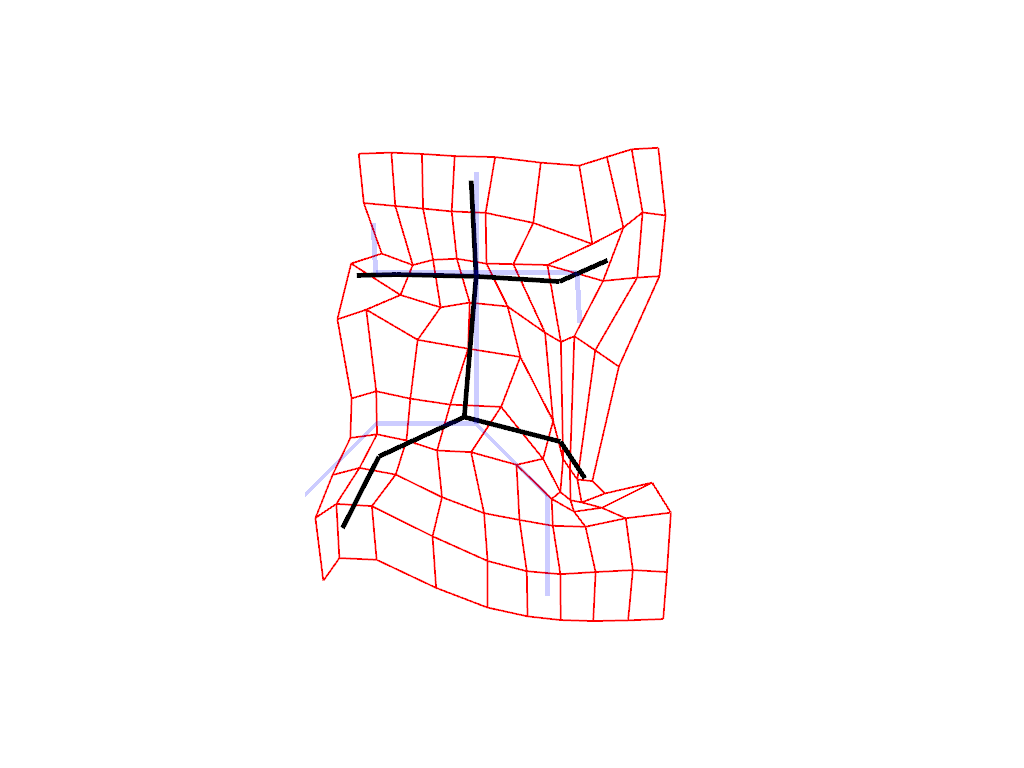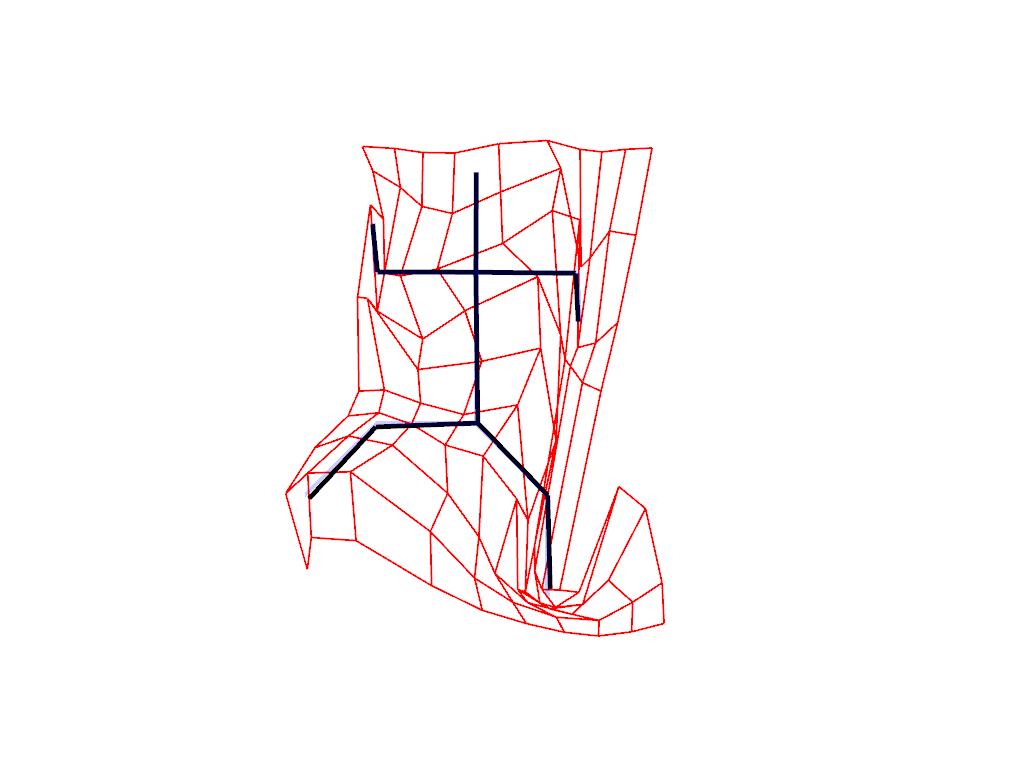
Extrinsic deformation

Extrinsic deformation is a kind of deformation that relies on the deformation of the ambient space, which is transferred to the shape. Intituively, you can think that you are twisting a sheet of paper on which the shape is drawn.

source.control_points = source.bounding_grid(N=10, offset=0.05)

model = sks.ExtrinsicDeformation(
    n_steps=6,
    kernel="gaussian",
    scale=1.0,
    control_points=True,
)

registration = sks.Registration(
    model=model, regularization_weight=0.1, **kwargs
)

registration.fit(source=source, target=target)

Initial loss : 5.37e+01
  = 5.37e+01 + 0.1 * 0.00e+00 (fidelity + regularization_weight * regularization)
Loss after 1 iteration(s) : 3.42e+00
  = 7.02e-01 + 0.1 * 2.72e+01 (fidelity + regularization_weight * regularization)
Loss after 2 iteration(s) : 2.72e+00
  = 1.30e-01 + 0.1 * 2.59e+01 (fidelity + regularization_weight * regularization)
Loss after 3 iteration(s) : 2.44e+00
  = 8.35e-02 + 0.1 * 2.36e+01 (fidelity + regularization_weight * regularization)
Loss after 4 iteration(s) : 2.23e+00
  = 6.60e-02 + 0.1 * 2.16e+01 (fidelity + regularization_weight * regularization)
Loss after 5 iteration(s) : 2.09e+00
  = 4.59e-02 + 0.1 * 2.05e+01 (fidelity + regularization_weight * regularization)

<skshapes.tasks.registration.Registration object at 0x7fa88f4ebc90>

Visualize the deformation

plot_extrinsic_deformation(
    source=source, target=target, registration=registration, animation=True
)

Intrinsic deformation

An intrinsic deformation is a deformation that is not transferable from one shape to another. It is defined as a sequence of small displacements of the points of the shape. In this setting, you can think of the shape as a puppet that you can deform thanks to a set of strings attached to its vertices.

In this example, we use the “as isometric as possible” metric, which tries to preserve the lengths of the edges of the shape.

model = sks.IntrinsicDeformation(
    n_steps=8,
    metric="as_isometric_as_possible",
)

registration = sks.Registration(
    model=model, regularization_weight=500, **kwargs
)

registration.fit(source=source, target=target)

Initial loss : 5.37e+01
  = 5.37e+01 + 500 * 0.00e+00 (fidelity + regularization_weight * regularization)
Loss after 1 iteration(s) : 6.99e+00
  = 4.08e+00 + 500 * 5.81e-03 (fidelity + regularization_weight * regularization)
Loss after 2 iteration(s) : 6.26e+00
  = 2.43e+00 + 500 * 7.65e-03 (fidelity + regularization_weight * regularization)
Loss after 3 iteration(s) : 6.02e+00
  = 2.12e+00 + 500 * 7.81e-03 (fidelity + regularization_weight * regularization)
Loss after 4 iteration(s) : 6.02e+00
  = 2.10e+00 + 500 * 7.84e-03 (fidelity + regularization_weight * regularization)
Loss after 5 iteration(s) : 6.02e+00
  = 2.10e+00 + 500 * 7.83e-03 (fidelity + regularization_weight * regularization)

<skshapes.tasks.registration.Registration object at 0x7fa89091af90>

Visualize the deformation

plot_intrinsic_deformation(
    source=source, target=target, registration=registration, animation=True
)