Intrinsic vs Extrinsic deformation

Intrinsic and extrinsic deformations are two different approaches to non-rigid deformation.

This example shows how both approaches differ on a simple 2D example.

import sys

import pykeops
from utils_karateka import (
    load_data,
    plot_extrinsic_deformation,
    plot_intrinsic_deformation,
    plot_karatekas,
)

import skshapes as sks

sys.path.append(pykeops.get_build_folder())

kwargs = {
    "loss": sks.L2Loss(),
    "optimizer": sks.LBFGS(),
    "n_iter": 5,
    "gpu": False,
    "verbose": True,
}

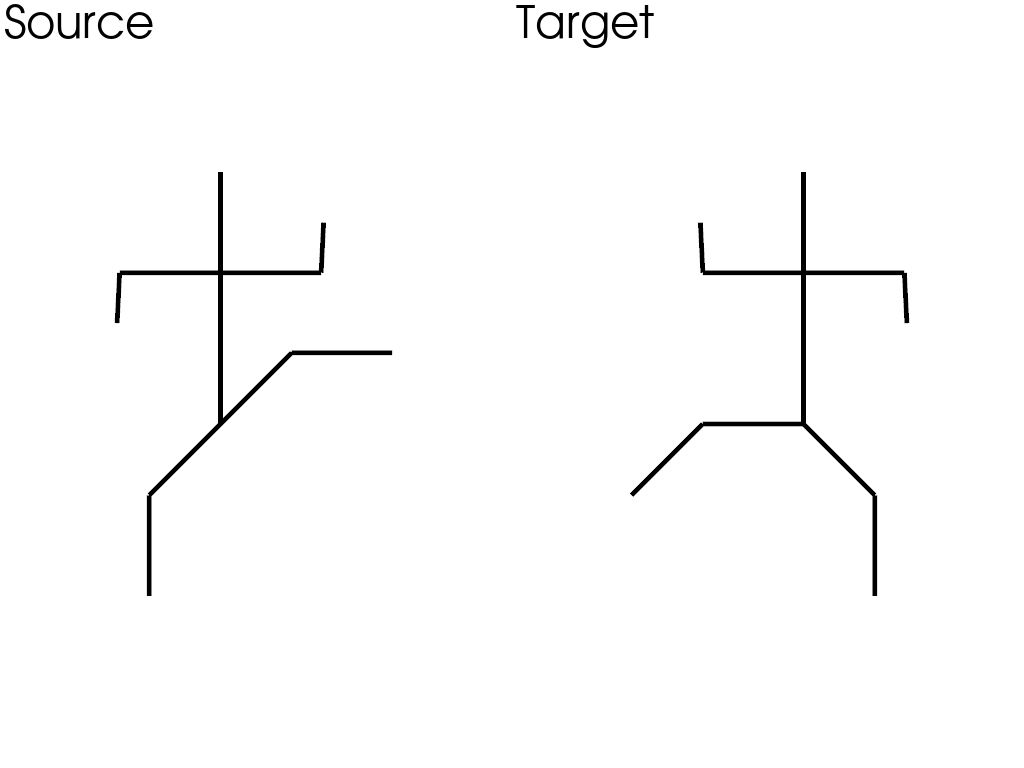
Load the data

source, target = load_data()
plot_karatekas()

Static Scene

Interactive Scene

Extrinsic deformation

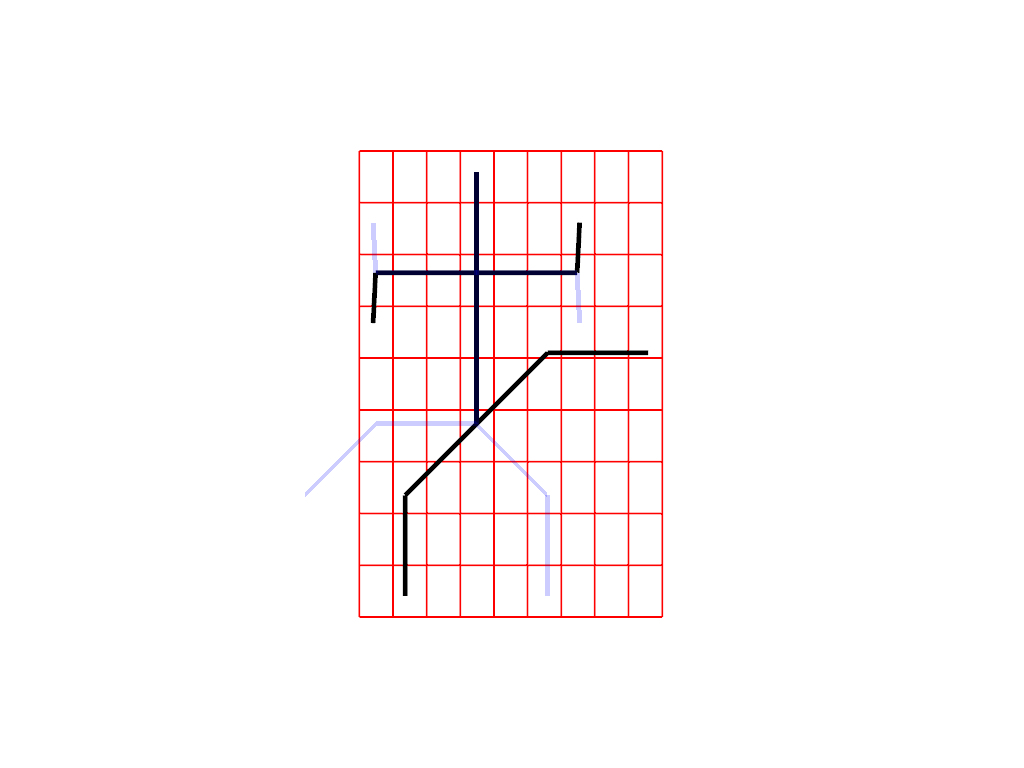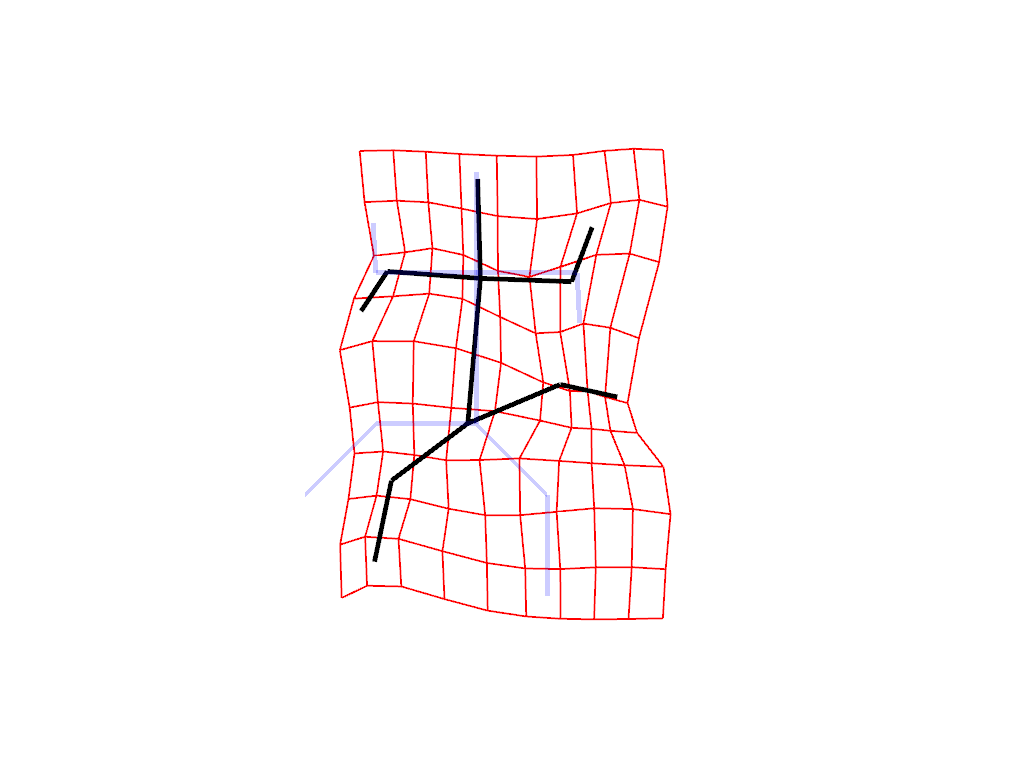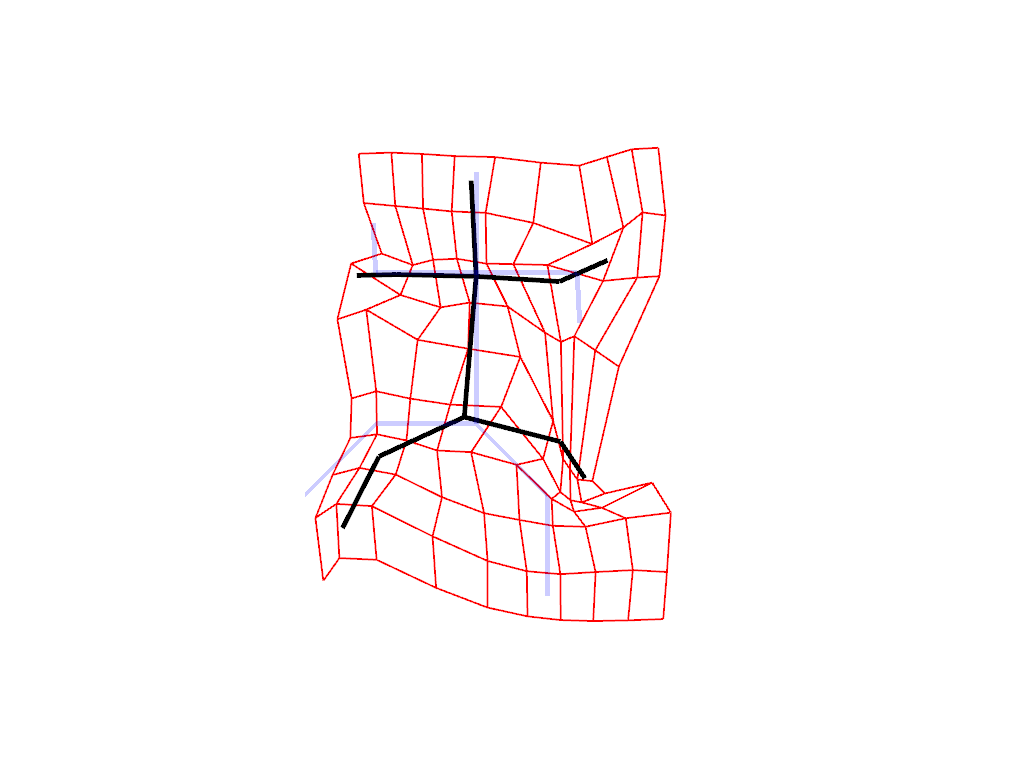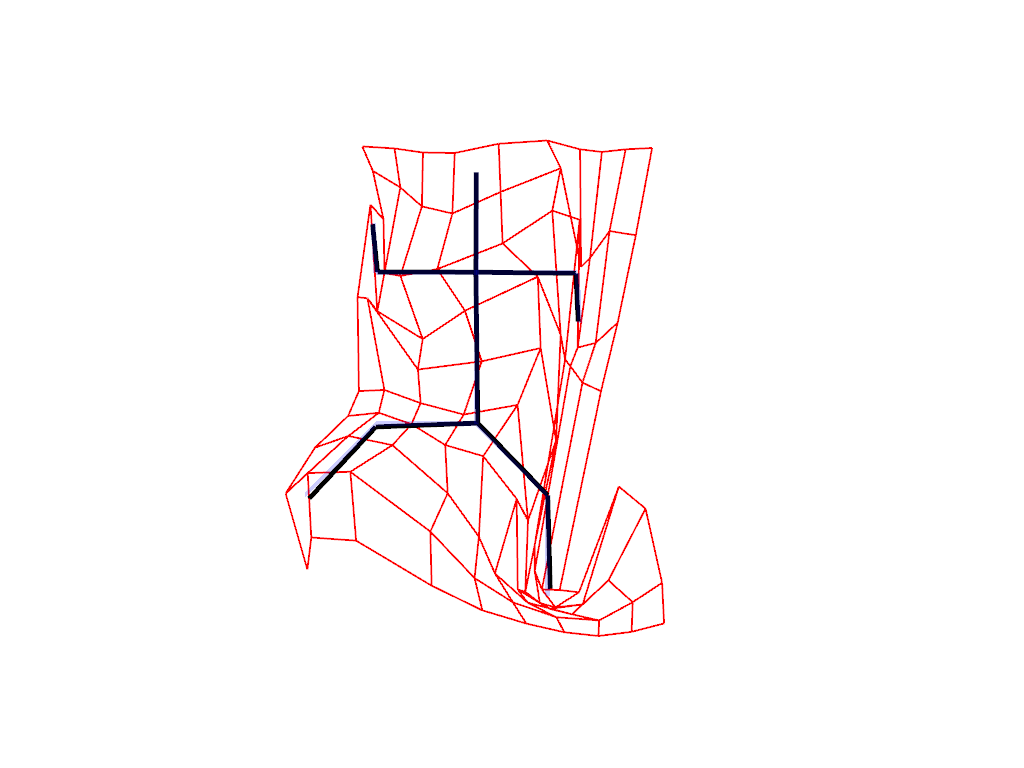
Extrinsic deformation is a kind of deformation that relies on the deformation of the ambient space, which is transferred to the shape. Intituively, you can think that you are twisting a sheet of paper on which the shape is drawn.

source.control_points = source.bounding_grid(N=10, offset=0.05)

model = sks.ExtrinsicDeformation(
    n_steps=6,
    kernel="gaussian",
    scale=1.0,
    control_points=True,
)

registration = sks.Registration(model=model, regularization_weight=0.1, **kwargs)

registration.fit(source=source, target=target)

[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula Exp(-Sum((a-b)**2))*c with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1) ... OK
[pyKeOps] Compiling pykeops cpp 699d776846 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula (-2*((a-b)*(d|c)))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), d=Var(3,2,0) ... OK
[pyKeOps] Compiling pykeops cpp f15bf17724 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula (2*((a-b)*(d|c)))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), d=Var(3,2,0) ... OK
[pyKeOps] Compiling pykeops cpp 5c5cdb61bf module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula Exp(-Sum((a-b)**2))*d with a=Var(0,2,0), b=Var(1,2,1), d=Var(3,2,0) ... OK
[pyKeOps] Compiling pykeops cpp e16cebc63a module ... OK
Initial loss : 5.37e+01
  = 5.37e+01 + 0.1 * 0.00e+00 (fidelity + regularization_weight * regularization)
[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula (-2*((a-b)*(f|d)))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), d=Var(3,2,0), f=Var(5,2,1) ... OK
[pyKeOps] Compiling pykeops cpp 55987b4211 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula (2*((a-b)*(f|d)))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), d=Var(3,2,0), f=Var(5,2,1) ... OK
[pyKeOps] Compiling pykeops cpp 463e746ff6 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula Zero(2) with  ... OK
[pyKeOps] Compiling pykeops cpp 0ddab92da3 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula Exp(-Sum((a-b)**2))*f with a=Var(0,2,0), b=Var(1,2,1), f=Var(5,2,1) ... OK
[pyKeOps] Compiling pykeops cpp d97d403f1a module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula (2*((d|c)*f)+-4*((a-b)*((d|c)*((a-b)|f))))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), d=Var(3,2,0), f=Var(5,2,1) ... OK
[pyKeOps] Compiling pykeops cpp f47179eff0 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula (-2*((d|c)*f)+4*((a-b)*((d|c)*((a-b)|f))))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), d=Var(3,2,0), f=Var(5,2,1) ... OK
[pyKeOps] Compiling pykeops cpp 84d406c697 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula (2*((f|(a-b))*d))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), d=Var(3,2,0), f=Var(5,2,1) ... OK
[pyKeOps] Compiling pykeops cpp b70aef3f0b module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula (2*((f|(a-b))*c))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), f=Var(5,2,1) ... OK
[pyKeOps] Compiling pykeops cpp 191aec60fd module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula (-2*((d|c)*f)+4*((a-b)*((d|c)*((a-b)|f))))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), d=Var(3,2,0), f=Var(5,2,0) ... OK
[pyKeOps] Compiling pykeops cpp 0728ba0c69 module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula (2*((d|c)*f)+-4*((a-b)*((d|c)*((a-b)|f))))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), d=Var(3,2,0), f=Var(5,2,0) ... OK
[pyKeOps] Compiling pykeops cpp c2758db4aa module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 1) of formula (-2*((f|(a-b))*d))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), d=Var(3,2,0), f=Var(5,2,0) ... OK
[pyKeOps] Compiling pykeops cpp bd79f5ff8e module ... OK
[KeOps] Generating code for Sum_Reduction reduction (with parameters 0) of formula (-2*((f|(a-b))*c))*Exp(-Sum((a-b)**2)) with a=Var(0,2,0), b=Var(1,2,1), c=Var(2,2,1), f=Var(5,2,0) ... OK
[pyKeOps] Compiling pykeops cpp cdc4e03da2 module ... OK
Loss after 1 iteration(s) : 3.42e+00
  = 7.02e-01 + 0.1 * 2.72e+01 (fidelity + regularization_weight * regularization)
Loss after 2 iteration(s) : 2.72e+00
  = 1.30e-01 + 0.1 * 2.59e+01 (fidelity + regularization_weight * regularization)
Loss after 3 iteration(s) : 2.44e+00
  = 8.35e-02 + 0.1 * 2.36e+01 (fidelity + regularization_weight * regularization)
Loss after 4 iteration(s) : 2.23e+00
  = 6.60e-02 + 0.1 * 2.16e+01 (fidelity + regularization_weight * regularization)
Loss after 5 iteration(s) : 2.09e+00
  = 4.59e-02 + 0.1 * 2.05e+01 (fidelity + regularization_weight * regularization)

<skshapes.tasks.registration.Registration object at 0x7ff414225cd0>

Visualize the deformation

plot_extrinsic_deformation(
    source=source, target=target, registration=registration, animation=True
)

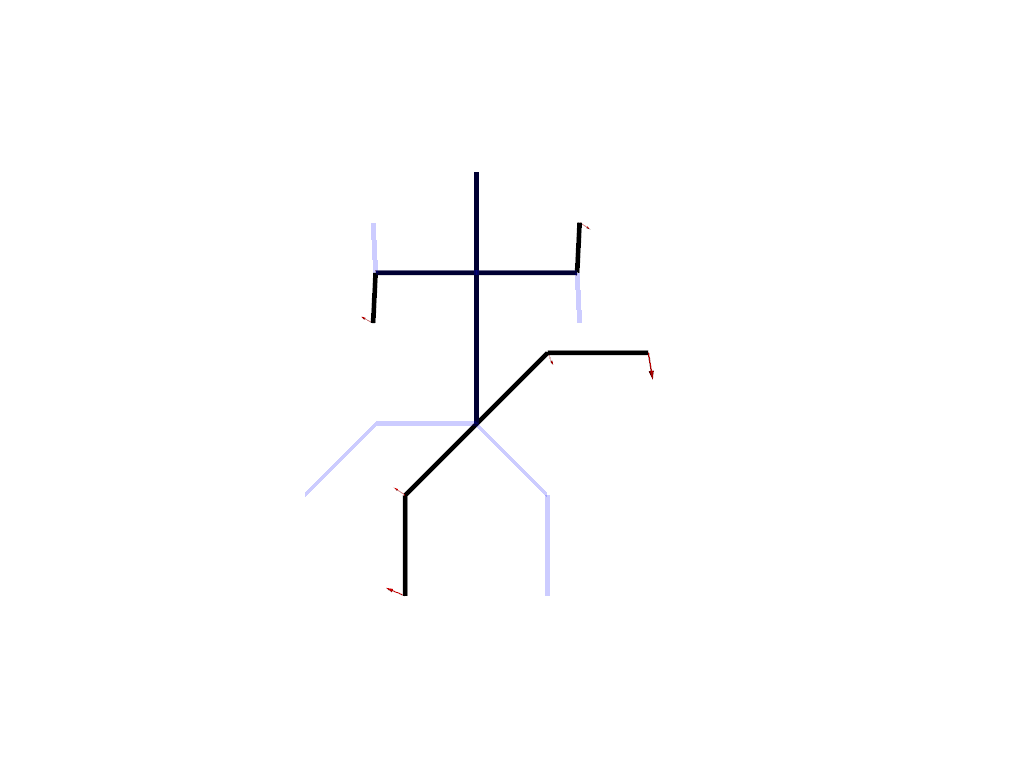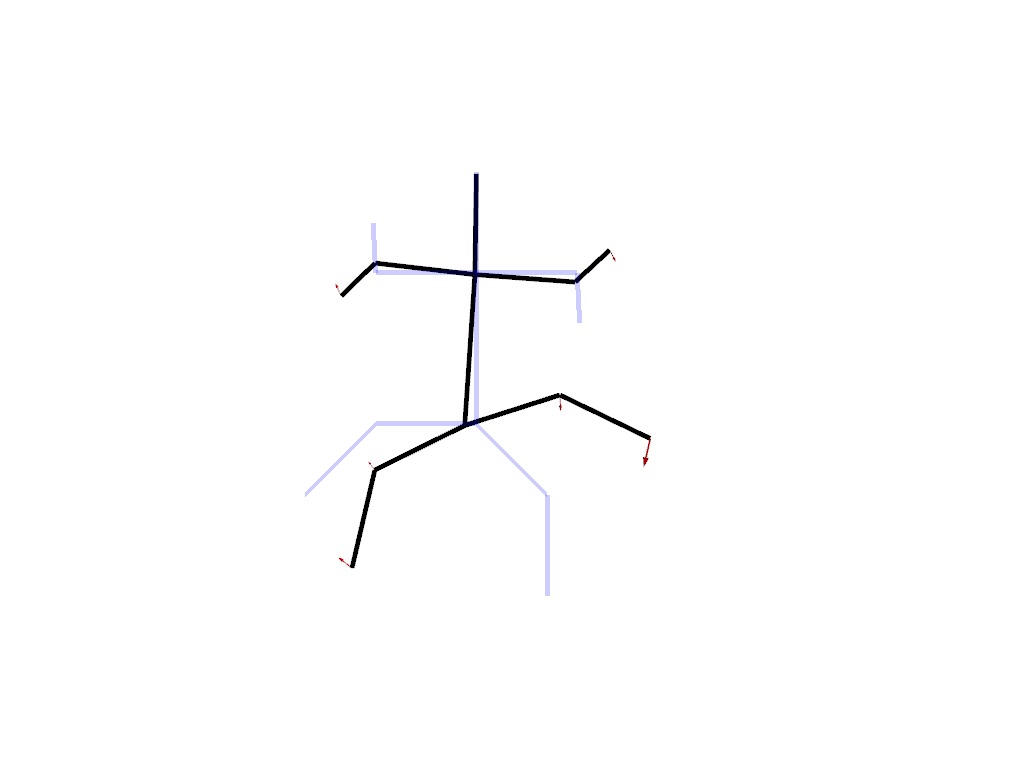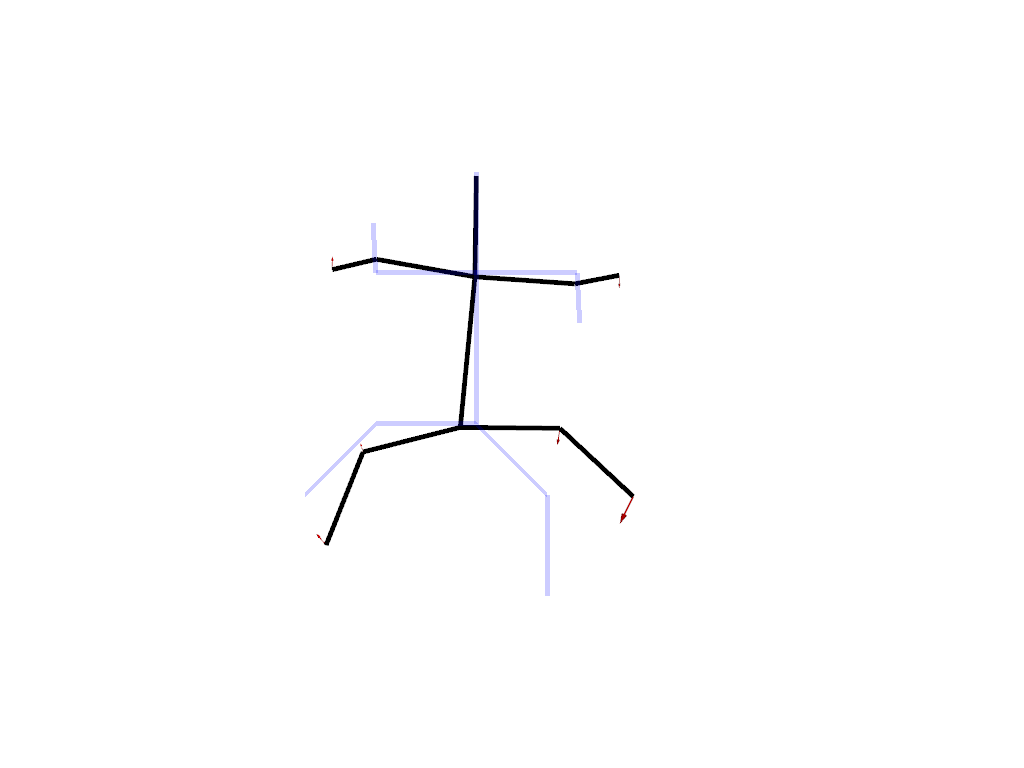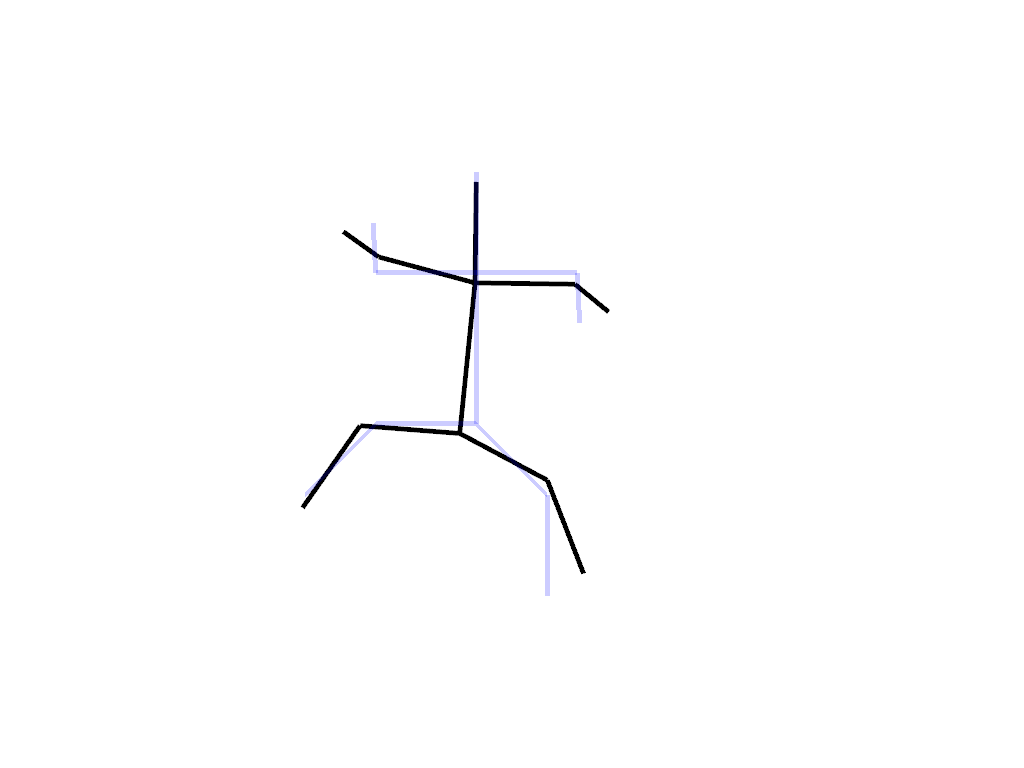
Intrinsic deformation

An intrinsic deformation is a deformation that is not transferable from one shape to another. It is defined as a sequence of small displacements of the points of the shape. In this setting, you can think of the shape as a puppet that you can deform thanks to a set of strings attached to its vertices.

In this example, we use the “as isometric as possible” metric, which tries to preserve the lengths of the edges of the shape.

model = sks.IntrinsicDeformation(
    n_steps=8,
    metric="as_isometric_as_possible",
)

registration = sks.Registration(model=model, regularization_weight=500, **kwargs)

registration.fit(source=source, target=target)

Initial loss : 5.37e+01
  = 5.37e+01 + 500 * 0.00e+00 (fidelity + regularization_weight * regularization)
Loss after 1 iteration(s) : 6.99e+00
  = 4.08e+00 + 500 * 5.81e-03 (fidelity + regularization_weight * regularization)
Loss after 2 iteration(s) : 6.26e+00
  = 2.43e+00 + 500 * 7.65e-03 (fidelity + regularization_weight * regularization)
Loss after 3 iteration(s) : 6.02e+00
  = 2.12e+00 + 500 * 7.81e-03 (fidelity + regularization_weight * regularization)
Loss after 4 iteration(s) : 6.02e+00
  = 2.10e+00 + 500 * 7.84e-03 (fidelity + regularization_weight * regularization)
Loss after 5 iteration(s) : 6.02e+00
  = 2.10e+00 + 500 * 7.83e-03 (fidelity + regularization_weight * regularization)

<skshapes.tasks.registration.Registration object at 0x7ff40c34fd50>

Visualize the deformation

plot_intrinsic_deformation(
    source=source, target=target, registration=registration, animation=True
)